V první části miniseriálu jsme sledovali stopu "starověké line" napříč zeměkoulí. Nejen první města, ale i první známé jazyky, egyptské hieroglyfy a sumerské klínové písmo se vyvinula podél této linie. Gigantické obrazce náhorní plošiny Nazca, Velká pyramida v Gíze, tisícileté chrámy ukryté v džungli i Velikonoční ostrov poodhalil část svých tajemství. Jde pouze o souhru podivných náhod, nebo je to fantastická skutečnost, která změní pohled na historii lidstva? Posuďte sami. Důkazy se množí…
ČÁST 9. - ŘEČ SINUSOIDY
Při pohledu na rotující zeměkouli vidíme rovník jako vodorovnou přímku, ale sledovaná "starověká linie" vykresluje nekonečnou sinusovou vlnu (obr. 1). Nejkratší vzdálenost mezi krajními body linie tvoří na položené mapě křivku.
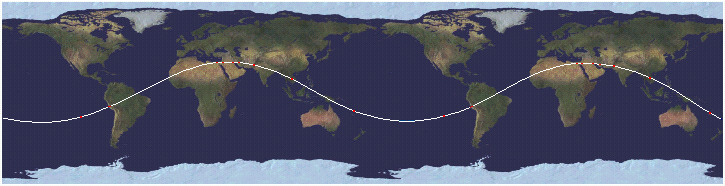
Obr. 1
Harmonické vibrace, elektrické impulsy a mnoho jiných přírodních jevů jsou založeny na takové sinusoidě. Tato pravidelně opakující se zvlněná linka se rovná obvodu Země. Horní i spodní výkmit sinusoidy zasahuje od svého středu až k 30° zeměpisné šířky. Připomeňme si, že hodnota 30° představuje polovinu výšky každé polokoule, neboli 1/2 poloměru Země.
Jestliže se špička vlny rovná 1/2 poloměru Země, pak se koeficient četnosti vlnových výkmitů rovná čtyřem pí. Pokud se vzdálenost vrcholových bodů sinusoidy (30° N až 30° S) rovná poloměru Země, pak se koeficient mezi opakováním výkmitů rovná dvěm pí.
ČÁST 10. - VELKÁ PYRAMIDA NA 30 ROVNOBĚŽCE
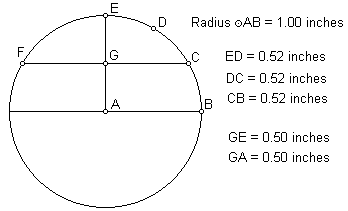Obr. 2
Tento kruh nemá žádnou orientaci a jeho průměr je zvolen náhodně (obr. 2). Vodorovná osa představuje rovník, úsečka FC se shoduje s 30 stupněm, bod D s 60 stupněm severní zeměpisné šířky a bod E leží na severním pólu. 30 stupeň je přesně jedna třetina části kružnice vymezené vzdáleností od rovníku k pólu a je umístěn přesně v polovině výšky severní polokoule. Tak jako Velká pyramida, leží i maximální zeměpisná šířka starověké linie blízko 30 rovnoběžky.
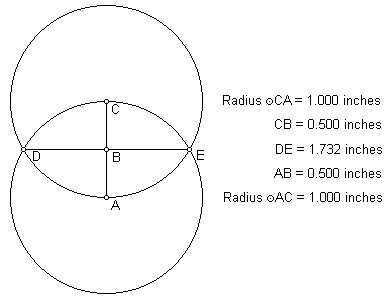Obr. 3
Tento obrázek ilustruje geometrický vztah obvodu Země k 30 rovnoběžce, známý jako "Vesica Pisces" (obr. 3). Schéma představuje průnik dvou kružnic v sledovaných bodech. Body DE nižšího kruhu jsou na 30 stupni severní šířky. Stejné body v horním kruhu jsou na 30 stupni jižní šířky.
Koeficient vzniklý vztahem největších vzdálenosti bodů a poloměru Země vyjadřuje hodnota 1,732 a 1, přičemž 1,732 je druhá odmocnina z hodnoty 3.
Obr. 5
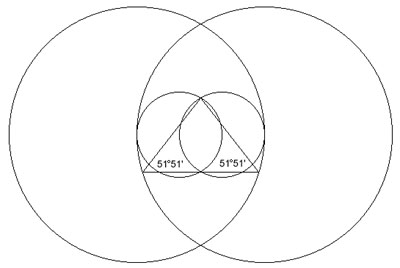
Paul Michell a Charles Henry zaznamenali vztah mezi Velkou pyramidou a symbolem "Vesica Pisces". Dva malé kruhy na tomto schématu mají průměr jeden palec a velké tři palce. Trojúhelník vzniklý v tomto schématu (obr. 5) má stejné úhlové hodnoty jako Velká pyramida v Gíze.
Obr. 6
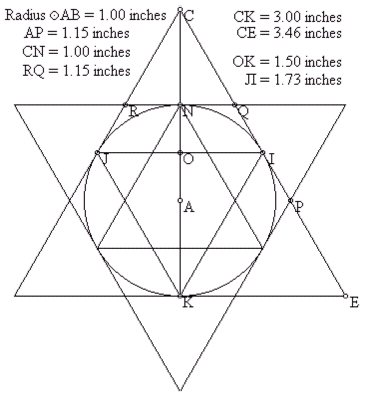
Kruh v tomto schématu (obr. 6) znázorňuje obvod Země s pólem umístěným na svislé ose. Poloměr kruhu má hodnotu 1 palec. Trojúhelníky sestrojené vně i uvnitř kruhu se dotýkají v bodě na 30 stupni a jejich vrcholy korespondují se severním pólem. Výška každého rovnostranného trojúhelníku je 87% vzdálenosti jeho strany.
3.00 / 3.46 = 0.87
1.50 / 1.73 = 0.87
1.00 / 1.15 = 0.87
Délka každé strany vnitřních trojúhelníků je shodná se vzdáleností linie vedené napříč Zemí na 30 stupni (JI). Tato hodnota se rovná 87% průměru Země.
1.73 / 2.00 = 0.87
Poloměr Země je také 87% vzdálenosti od jejího středu k průsečíkům na vnějším trojúhelníku (AP, AQ, AR..)
1.00 / 1.15 = 0.87
Délka řecké stopy byla stanovena v době, kdy nebyla známa velikost Země, tak jako tomu bylo i u stopy klasické. Standardní délková míra 1 stopy činí 87% původní - řecké stopy.
Také délka jedné míle byla stanovena mnohem dříve, než byly známy rozměry zeměkoule a činí 87% námořní míle, která byla specificky vypočítána s ohledem na velikost Země. 1 námořní míle se rovná jedné minutě, 60 námořních mil jednomu stupni a 5 400 mil 90 stupňům zeměpisné šířky mezi rovníkem a pólem. Vzdálenost rovníku k pólům je 6 215 mil.
5 400 / 6 215 = 0,87
Jedna minuta zeměpisné šířky se rovná 1 námořní míli v jakékoliv zeměpisné délce. Na rovníku se 1 minuta zeměpisné délky rovná 1 námořní míli, avšak ve vyšší šířce se vzdálenost jedné minuty zmenšuje.
Přímka vedená skrz Zemi v bodě 30 rovnoběžky má hodnotu 87% jejího průměru. Obvod kolem Země na 30 stupni je 87% obvodu na rovníku a každá minuta zeměpisné délky tamtéž je 87% délkové minuty na rovníku. Výsledkem je, že jedna námořní míle, rovná jedné minutě zeměpisné délky na rovníku, má stejnou hodnotu jako standardní míle a jedna minuta na 30 stupni.
Aktuálně přijatá hodnota pro rovníkový průměr Země je 7 926 mil a poloměr 3 963 mil. Poměr zemského poloměru k přímce vedené skrz Zemi na 30 stupni je 1 : 1,732.
3 963 mil x 1,732 = 6 864 mil (přímka vedená skrz Zemi na 30 stupni)
6 864 mil x 3,14(pí) = 21 564 mil (obvod Země na 30 stupni)
21 564 mil / 360 stupni = 59,9 míle (jeden stupeň zem. délky na 30 stupni)
59,9 míle / 60 minutami = 0,998 míle (minuta zem. délky na 30 stupni)
Jako alternativní důkaz doplňuji, že aktuálně přijatá hodnota pro rovníkový obvod Země je 24 902 mil. Obvod na 30 stupni má hodnotu 87% délky zemského rovníku.
24 902 mil x 0,87 = 21 664 (Obvod na 30 stupni je 87% rovníkové délky)
21 664 mil / 360 stupni = 60,1 míle (jeden stupeň zem.délky na 30 stupni)
60,1 míle / 60 minutami = 1.00 míle (jedna minuta zem.délky na 30 stupni)
ČÁST 11. - NAPŘÍČ ZEMÍ
Obr. 7
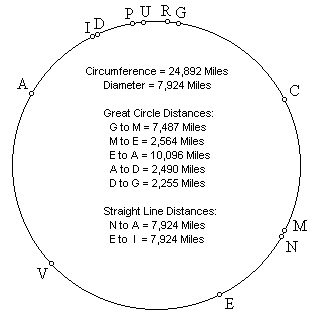
Linie starověkých míst si můžeme představit jako kruh, protože všechna místa jsou na přímce kolem středu Země (obr. 7). Vzdálenosti prehistorických staveb na velké kružnici vychází ze skutečně naměřených vzdáleností mezi nimi.
G = The Great Pyramid
C = Cape Verde Islands
M = Machu Picchu
N = Nazca
E = Easter Island (Velikonoční ostrov)
V = Anatom Island
A = Angkor Wat
I = Indus Valley
D = Mohenjo Daro
P = Perseopolis
U = Ur
R = Petra
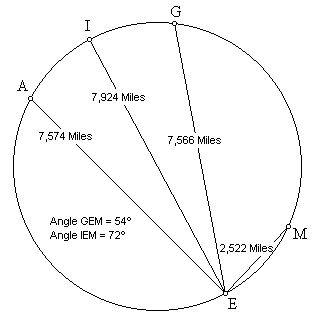
Přímky jsou vedeny skrz Zemi a spojují Velikonoční ostrov s Machu Picchu, Velkou pyramidu s Angkor Wat a údolím Indu, nebo opačně. Součet vzdáleností přímky vedené napříč Zemí z Angkor Wat k Velikonočnímu ostrovu (7 574 mil) a přímky z Velikonočního ostrova do Machupicchu (2 522 mil) se rovná vzdálenosti na velké kružnici (povrchová vzdálenost) mezi Angkor Wat a Velikonočním ostrovem (10 096 mil). Přímka napříč Zemí vedená z Velké Pyramidy k Velikonočnímu ostrovu (7 566 mil) je třikrát delší, než vzdálenost Velikonočního ostrova k Machu Picchu (2 522 mil). Přímka vedená z Velikonočního ostrova k protilehlému bodu v údolí Indu (7 924 mil), což je také průměr Země, je 3,1416 krát delší než vzdálenost z Velikonočního ostrova do Machu Picchu (2 522 mil), což je precizní vyjádření hodnoty konstanty pí (obr. 8).
Obr. 8
Předtím, než jsme se naučili vypočítat obvod Země násobením konstanty 3,1416 jejím průměrem, bylo možné získat tutéž hodnotu pouhým násobením vzdálenosti Velikonočního ostrova do Machu Picchu hodnotou pí.
Vnitřní úhel mezi linkami z Velikonočního ostrova k Machu Picchu a údolí Indu je 72 stupňů. Úhel linek mezi Velikonočním ostrovem, Machu Picchu a Velkou pyramidou je 54 stupňů.
Linky spojující Velikonoční ostrov, Velkou pyramidu a angkorské chrámy poblíž Rolous tvoří rovnoramenný trojúhelník se stranovými úhly 72,9 stupňů. Základna tohoto trojúhelníku (AG) je dlouhá 4 462 mil a výška (HE) je 7 220 mil. Délka základny násobená konstantou fí (1,618) určuje výšku trojúhelníku (obr. 9).
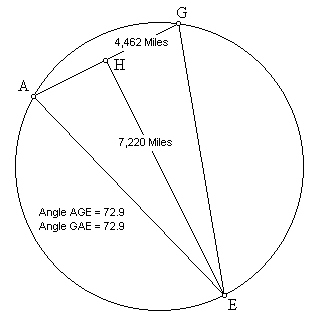Obr. 9
4 462 mil x 1,618 = 7 220 mil
Délka každé základny Velké pyramidy je 755,6 stopy a šikmá výška každé strany je 611 stop. Jedna polovina délky základny násobená hodnotou fí (1,618) se rovná její šikmé výšce (obr. 10).
755,6 stopy / 2 = 377,8 stopy
377,8 stopy x 1.618 = 611 stop
Jak je zřejmé z nákresu, protilehlý bod k Velikonočnímu ostrovu je v údolí Indu a protilehlý bod plošiny Nazca je chrámové město Angkor. Spojovací linky napříč Zemí tvoří dva rovnoramenné trojúhelníky se stranovými úhly 72,9 stupňů. Shodné úhly má i trojúhelník tvořený Velikonočním ostrovem, Angkorem a Velkou pyramidou. Délka základny těchto trojúhelníků násobená konstantou fí se rovná jejich výšce.
2 337 mil x 1,618 = 3 782 mil
Poměr základny k šikmé výšce Velké pyramidy je přesně dvakrát větší než poměr základny a výšky trojúhelníků sestrojených napříč Zemí z Velikonočního ostrova, Nazcy; Angkoru, údolí Indu a středem Země.
Jestliže je vzdálenost mezi Velkou pyramidou a Angkorem přibližně 20% obvodu kruhu, pak jsou odděleny úhlem přibližně 72 stupňů.
Jestliže je vzdálenost Velké pyramidy k Velikonočnímu ostrovu přibližně 40% obvodu a vzdálenost Angkoru k Velikonočnímu ostrovu také 40%, pak jsou Velká pyramida a Angkor vzdáleny od Velikonočního ostrova 144 stupňů na velkém kruhu.
Číslo 72 a jeho varianty 54, 108 a 144 úzce souvisí s dispozičními rozměry staveb jako je Velká pyramida nebo Angkor. Počet postavených chrámů kolem Angkoru je 72, číslo 54 vyjadřuje počet vysokých soch v Angkor Tom. Použití těchto čísel převažuje také ve starověkých spisech a folklóru v okolí těchto míst. Číslo 54 souvisí s hodnotou 72. Hodnota 72 vznikne součtem čísel 36 i 108, kterou podělíme dvěma (54). Číslo 72 je také spojené s astronomickým fenoménem zvaným precese, kde 72 let je časový úsek posunu souhvězdí na noční obloze o jeden úhlový stupeň.
Poloměr jakékoliv koule krát 2pí se rovná jejímu obvodu. Neobvyklý sklon stěn Velké pyramidy 51 stupňů (jedinečný mezi egyptskými pyramidami) nebyl zvolen náhodou. Výška jehlanu krát 2pí se rovná obvodu pyramidy. Kvůli těmto skutečnostem se usuzuje, že byla Velká pyramida postavena jako přesný model jedné polokoule Země v poměru 43 200 : 1.
V existujícím šedesátkovém (60) systému, tvořeném sekundami a minutami, používaném pro čas i pro stupně vzdáleností na Zemi je číslo 43 200 velmi podstatné. Jedna sekunda krát 60 se rovná jedné minutě, krát 60 se rovná jedné hodině, krát dvanáct se rovná 12 hodinám. Sledujme další vztahy. 43 200 sekund se rovná polovině dne. 30 sekund krát 2 se rovná minutě, krát 60 se rovná jeden stupeň, krát 360 se rovná obvodu Země. Jedna polovina minuty zeměpisné šířky krát 43 200 se rovná obvodu Země!
Ve druhém století př.n.l. řecký matematik Archimedes napsal stať, ve které cituje nejranější řecké matematiky (kteří jako on také studovali v Alexandrii a Heliopolisu) v níž vypočítal, že Slunce okupuje 1/720 plochy kde obíhají souhvězdí (oblohy). 720 krát 60 se rovná 43 200. Počet precesí je 72, krát jednotka času 60, krát deset se rovná číslu 43 200.
Jestliže vztah čísla 43 200 k Velké pyramidě není jen shoda okolností, pak její stavitelé museli znát velikost Země.
Tento vztah, právě tak jako přítomnost čísla 72 a jeho variant, vysledovaný v mnoha starověkých stavbách a spisech, naznačuje znalost doby trvání precese a rovnodennosti. V každém případě je existence těchto čísel a použití geometrických vztahů v interiérech u nejstarších staveb prokazatelná.
-pokračovanie-
Všetky časti postupne nájdete na tejto adrese.
http://home.hiwaay.net/~jalison/
Fyzikální a matematické tabulky
Preklad: Jiří Matějka
Zdroj: http://www.wmmagazin.cz/
http://www.dunres.sk/projects/_ee/clanky.php?id=45
Súvisiace:
Editoriál: PLANETÁRNA MRIEŽKA
http://www.miesta.net/clanok/editorial-planetarna-mriezkaOČKO: Planetárna mriežka - Posvätné chrámy
http://www.miesta.net/clanok/ocko-planetarna-mriezka-posvatne-chramyDôkazy pradávnej vedy?
http://www.miesta.net/dokazy-pradavnej-vedy
